Shmoocon 2012 "Blocky" (RE 400) Writeup

2012-02-07

The Ghost In The Shellcode competition had a really cool challenge in the RE category called Blocky. It's a minecraft world where the game elements are used to perform a bitwise function on the input and compare the output to a fixed value. The correct input (inverse) is the "launch code" as requested by the level.

My friend Scott has written an insane guide on how to extract the circuit from the game, and how to solve it using linear algebra. His complete writeup is here and a slightly abridged version follows below. Then we'll solve it a second way by converting the circuit to a SAT instance and solving it with picosat.

Get Creative

First, modify the world to be in Creative mode. Now it's trivially easy to add or remove any type of block from the world. I stripped away the north half of the building so I could fly straight down to the switches, and I also removed the entire TNT cannon since it was covering the "signal bus" coming straight from the switches. Also, I removed the tamper-resistance line just because I didn't want it confusing me as I traced out the circuit. But the most important reason to be in Creative mode is so that you can easily label your traces without having to acquire resources to make colored wool or whatever you use for your labeling scheme.

Minecraft Circuits

Circuits are made using Redstone Powder (often just called Redstone), Redstone Torches, Redstone Repeaters, and Switches. See this wiki link for more information.

• Redstone Powder, or just Redstone, is the "current carrying" element, the wiring.
• Redstone Torches (not to be confused with normal Torches) can power Redstone circuits. They burn indefinitely. They can also be switched on or off if they are mounted on top of or on the side of a block. This creates an inverter.
• Switches and Redstone torches can only power a Redstone circuit for a distance of 15 blocks. Redstone Repeaters are like line buffers that will retransmit their input signal, allowing you to carry a circuit indefinitely as long as you space repeaters every 16 blocks or closer. Also, like electrical line buffers, they are unidirectional -- they act like diodes, passing the signal only in the direction of their "arrow".
• Redstone Repeaters are also configurable delay elements. This behavior is not used in this circuit.
• Blocky only uses NOT, AND, and XOR gates

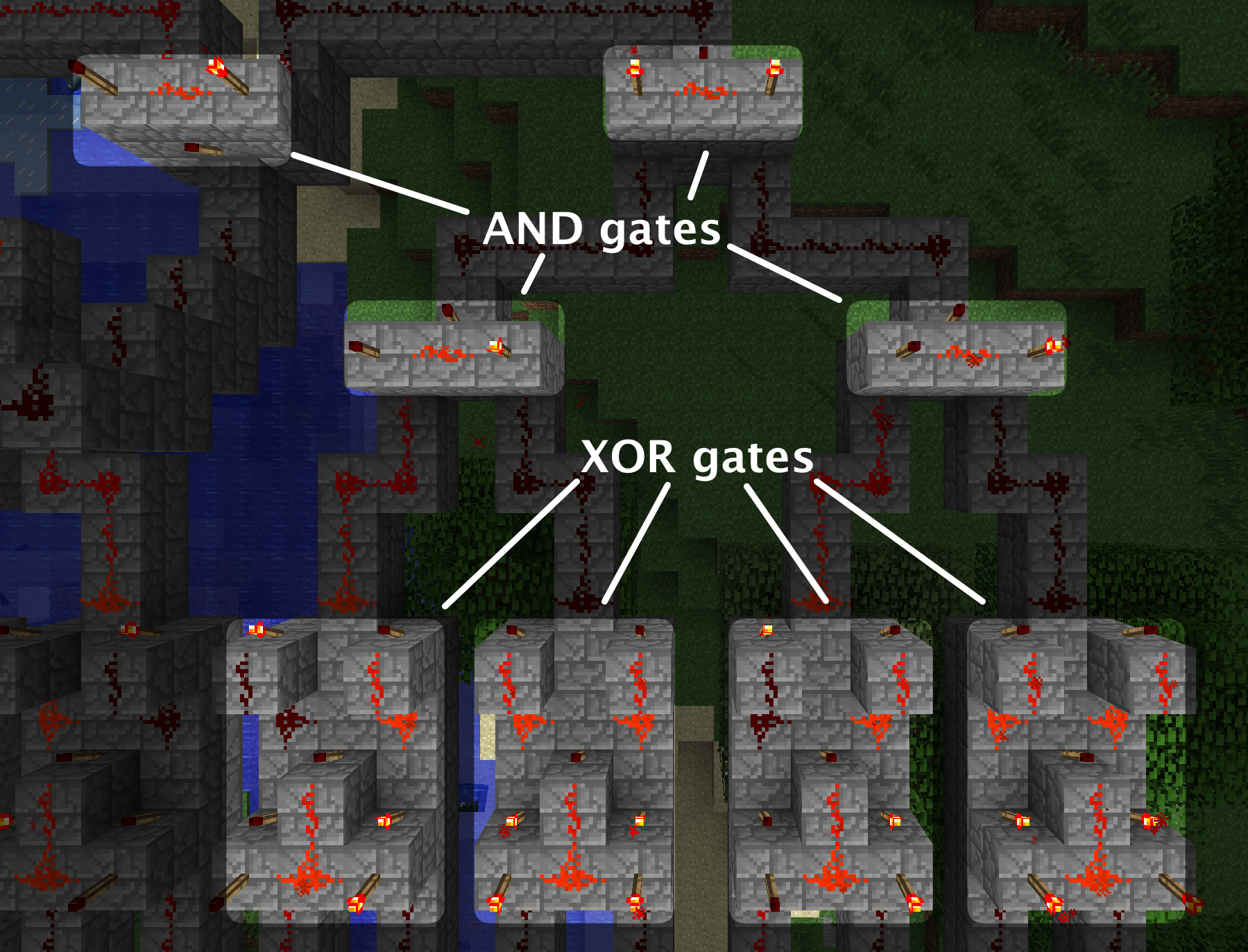
Labelling

I used colored wool blocks to come up with a color code for the circuit traces. The 4 gray-scale wool blocks (white, light-gray, dark-gray, and black) grouped 6 bits, and each line in the groups were denoted by Red, Orange, Yellow, Green, Blue, and Purple. I also found it helpful to use another visually distinctive block (such as Gold) to label a line that had been inverted prior to entering a logic gate. In my "colored wool" notation, Switch 'Bit 0' is White-Red, down to 'Bit 23' = Black-Purple.

First I labeled all the switches, then I traced out every line to the input of a logic gate. I followed all branches of the switch lines. I didn't bother labeling the outputs of logic gates because they were much easier to follow as busses than the input lines were.

Analysis

If you fly up high and look down at the circuit, you'll see that the West side is 24 XOR gates, with their outputs being bussed together quite nicely North, along the Northern edge of the circuit, and then fanned out nicely to the gates on the East side. The East side is a collection of another 24 XOR gates, whose outputs are pairwise AND'ed together to a single line, the one that fires the TNT cannon.

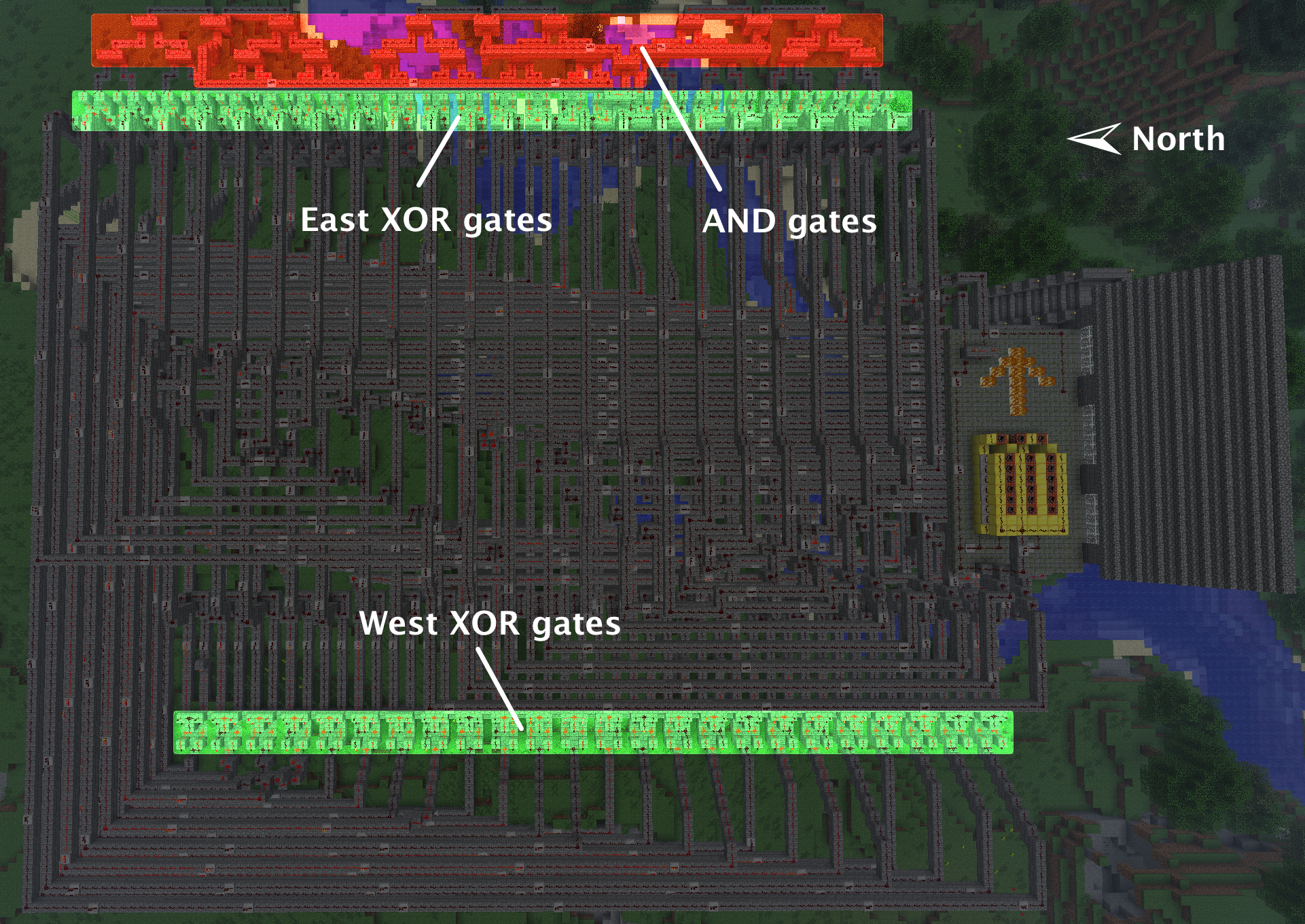
So at the most basic level, the gates appear to describe the following equation:

where "a ^ b" is the West side XOR group, which is XOR'ed with c on the East side. a, b, and c are some unknown functions of the input word (switches).

That describes all the uses of the AND and XOR gates, but what about the NOT gates? They just invert some of the inputs to the XOR gates. Realizing that XOR'ing with 1 is the same as inverting a bit (NOT) and XOR'ing with 0 is the same as, well, a wire or a no-op, we can collect up the inverters (and non-inverted lines) to form XOR masks on the input lines to the actual XOR gates. Thus we can see that our functions (a,b,c) are:

where P, Q, and R are constants, and x, w, and z are the input lines to the gates. So the circuit is now described by:

Starting on the West side XOR group, I chose the Southern-input (left, if you're looking at the input side of the gate) as "a", and the Northern (right) input as "b". Starting at the Northern-most end, you see !"White-Red" ^ !"DarkGray-Blue" (where '!' denotes NOT). That's !Bit0 ^ !Bit16. Moving over South to the next XOR gate, you see "White-Orange" ^ !"DarkGray-Purple", or Bit1 ^ !Bit17.

This pattern of XOR'ing Bit(n) with Bit(n+16 mod 24) -- ignoring the NOT's -- continues for the entire West side XOR gate group. Letting our 'x' represent the left-inputs of the gates, and 'w' represent the right inputs of the gates, x is just the input word, and w is the input word rotated left (circular shift left, barrel rotate left, whatever you want to call it) by 8 bits. In C, it could be written as:

Collecting up the Gold block constants (where Gold blocks are 1, and no Gold block is 0), we find P = 0xC7F101 and Q = 0xC123AB. This looks promising. 0xC7F101... "CTF 101"... and 0xC123AB is just 0xABC123 left-rotated by 8 bits. We're on the right track.

Movin' on up to the East side (to a deluxe apartment in the sky... sorry), we see the bus of lines from the West side XOR gates fans back out in an orderly fashion without any more bit rotations or inverters (NOT gates), into the North input of each East side XOR gate. So only the Southern (right) inputs of the East XOR gates have any inversions.

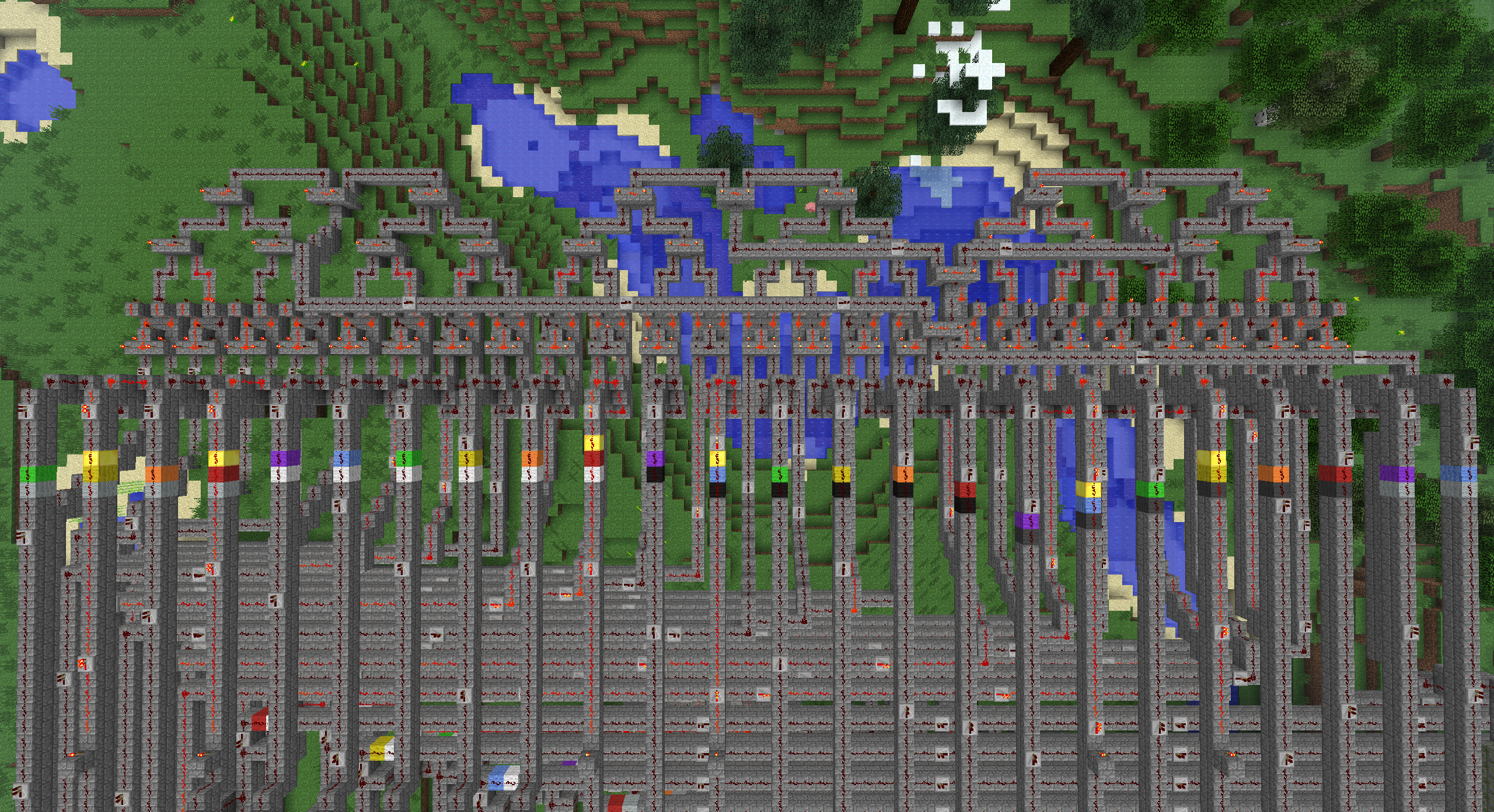
Looking at Southern-most XOR gate on the East side, we see "LightGray-Blue" ^ [the output of the Northern-most West side XOR gate]. "LightGray-Blue" corresponds to Bit10, and after verifying the color pattern, we see that the East side XOR gates are just [West side XOR outputs] ^ rotl24(x, 14) (again, ignoring the NOTs on the rotated inputs). Collecting the XOR-mask bits, we find R = 0x505050. That looks like a sensible sentinel value, so let's assume we're still tracking correctly.

The Equation

Okay, we're done with Minecraft for now. Our circuit can be described by the following equation:

Now, since the equation only contains XOR's, and since XOR is commutative, let's rewrite and reduce this to:

If we XOR both sides by 0x5682FA to eliminate it from the left hand side, we have:

or

Solve for x, set the switches correspondingly, and light the TNT cannon up.

A simple brute-force solver yields x = 0x37A8D8; this is the only value of x that will fire the cannon.

Let's write the equation as y = Ax, where y replaces the constant, both x and y are column vectors of the bits of the input and output, respectively, and A is the transformation matrix that describes the rotations in the original equation. Going bit-by-bit, we see that y[0] = x[0] ^ x[16] ^ x[10]. For the next bit of output, y[1] = x[1] ^ x[17] ^ x[11]. It's a pretty obvious pattern: y[n] = x[n] ^ x[n+16 (mod 24)] ^ x[n+10 (mod 24)]

Observation: All of the even-order bits of the output are dependent upon only even-order bits of the input. In our equation, only the even-order bits keep to themselves, and the odd-order bits mingle with their own kind. This means that this 24-bit tranformation from x to y is functionally identical to interleaving (Mortonizing) the 12-bit transformation f' : x' -> y' = x' ^ rotl12(x', 4) ^ rotl12(x', 7) when applied separately to the even-order bits and the odd-order bits of the original 24-bit space. Thus, this isn't really a 24-bit problem at all. It's a 12-bit problem, just applied to two input values (that happen to be the de-interleaved bits of x), producing two output values and interleaving them to produce a 24-bit Morton number. If this were a 64-bit key we were looking for, reducing the problem to solving it for two 32-bit numbers would be critical to brute-forcing the answer within the timeframe of a CTF competition. As it is, 24 bits takes a fraction of a second to brute force. So it's interesting, but not necessary for solving.

Keygenning with Linear Algebra

Anyways, back to the transformation matrix A. Using simple Gaussian Elimination to find the matrix B that gives x = By, we find that:

A keygen that doesn't reduce this far and leaves it in matrix multiply form is available here

Keygenning with SAT

XOR'ing the x and the two rotations, we can write an equation for each bit of the output (targetting 0xA97D05)

Now for every gate is introduced a new variable representing its output. Then a precomputed CNF is substituted that evaluates to true when the gate is operating properly. This is called the Tseitin transformation and I threw up a description and a small example on Wikipedia.

The new formula is equisatisfiable and has more variables the the original, but its length has grown linearly compared to the input formula, vs using De-Morgan and distribution laws which can have exponential expansion of the input formula. The final "top output" of each new circuit can then be placed in its own clause (possibly complemented) to aim it at a particular output.

Equation 0 converts to:

Equation 1 converts to:

And so on for all 24 equations. Since all of these must be true at the same time, you can just "AND" them all together, resulting in:

Cool formula huh? There are 72 variables and 216 clauses. It's definitely in CNF. The only thing left to do is put it in DIMACS format so that a sat solver can actually consume it and produce us an answer! Given to Picosat, the output is:

The integers [1,72] refer to the variables we made. Positive values mean "true" while negative values mean "false". We discard assignments to the dummy "gate" variables which leaves us with:

Ordering the bits to get 001101111010100011011000. Separate the nibbles to get 0011-0111-1010-1000-1101-1000. Convert to hex to get 0x37A8D8.

Conclusion

I've loved digital logic ever since EEL3701 so reading about what Scott found in this challenge and seeing his screenshots really got me excited. SAT solving is something I've been reading and learning about recently and this was the perfect opportunity to put that nascent knowledge to the test.